Sistemes Discrets

En aquesta pràctica veurem com es comporten els sistemes discrets definits genèricament com

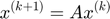$$ x^{(k+1)} = A x^{(k)}$ essent A una matriu lineal.

El mètode de la potència
Exemple: la successió de Fibonacci
Valors propis complexes 2x2
Aplicació: Dinàmica de la Població de Mussols Americans
Càlcul Pràctic dels coeficients de la matriu d'interaccions

El mètode de la potència

Quan iterem un sistema dinàmic discret, el comportament dels punts obtinguts està relacionat amb els valors propis de la matriu A. En particular, el valor propi de mòdul màxim (dominant) es pot calcular a partir de com varia el mòdul dels nous iterats (mètode de la potència)

A=[1, 2; 3, 4];
vaps=eig(A)
x=[1;1]; %punt inicial
N=10; %numero d'iteracions, depen del valor del vap màxim
for i=1:N
    xNext=A*x;
    x=xNext/norm(xNext);
end
eigMax = max((A*x)./x)

vaps =

   -0.3723
    5.3723


eigMax =

    5.3723

Exemple: la successió de Fibonacci

Aquesta és una coneguda successió que podem expressar com

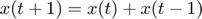$$x(t+1)= x(t) + x(t-1)$ (Fibonacci)

Per estudiar-la la passem a un sistema 2D fent:

$$ x_1(t+1) = x_1(t) + x_2(t)$

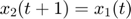
$$ x_2(t+1) = x_1(t)$

és conegut que la proporció entre dos iterats consecutius de la successió de Fibonacci tendeix a la raó aurea (golden ratio): $$\frac{1+\sqrt{5}}{2}$

A=[1,1;1,0]; %matriu de Fibonacci
eig(A)
x=[0; 1]; %valors inicials
N=10; %numero d'iteracions, depen del valor del vap màxim
for i=1:N
    xNext=A*x;
    x=xNext;
end
eigMax = max((A*x)./x);
valorExact= (1+sqrt(5))/2; % Golden ratio
[eigMax, abs(valorExact-eigMax)]

ans =

   -0.6180
    1.6180


ans =

    1.6182    0.0001

Valors propis complexes 2x2

A=[0.5, 0.7; -0.7, 0.5];
eig(A)
x=[0.1;0.1]; %punt inicial
X=x;
N=100; %numero d'iteracions
for i=1:N
    xNext=A*x;
    x=xNext;
    X=[X,x]; %guardem tots els iterats
end
% dibuixem les iteracions
plot(X(1,:),X(2,:),'.-')

ans =

   0.5000 + 0.7000i
   0.5000 - 0.7000i

Aplicació: Dinàmica de la Població de Mussols Americans

(Trobareu l'enunciat als Exercicis de la Unitat 4. Sistemes lineals discrets. Problema 11.)

a = 0.3;  %taxa de supervivència joves
b = 0.18; %taxa dels que arriven a subadult (18%)
c = 0.71; %taxa de supervivència dels subadults
d = 0.94; %taxa de supervivència dels adults

A=[0    ,0    ,a;
   b    ,0    ,0;
   0    ,c    ,d;
   ];

eig(A)

x=[100;100;100]; %punt inicial
X=x;
N=50; %numero d'iteracions
t=0:N;
for i=1:N
    xNext=A*x;
    x=xNext;
    X=[X,x]; %guardem tots els iterats
end
plot(t,X(1,:))
hold on;
plot(t,X(2,:))
plot(t,X(3,:))

ans =

  -0.0200 + 0.1968i
  -0.0200 - 0.1968i
   0.9799 + 0.0000i

Càlcul Pràctic dels coeficients de la matriu d'interaccions

Si es conèixen els coeficients de la matriu A llavors el problema es redueix a fer-ne una simulació d'evolució temporal com hem vist anteriorment. A la pràctica això voldria dir que hem de coneixer les interrelacions entre els individus i això normalment és molt difícil d'aconseguir. A la pràctica el que podem fer és un cens d'individus en N+1 instants de temps on N és la mida de la matriu A.

Llavors A=[X(2),X(3),...,X(N+1)]*inv[X(1),X(2),...,X(N)].

Per exemple, en el cas anterior N=3, faríem el contatge dels mussols en 4 temporades consecutives. X(1),X(2),X(1),X(4) i sabem que, assumint un model lineal, X(4) ha de ser combinació lineal de X(1),X(2),X(3) (sempre que siguin linealment independents). Llavors el sistema per calcular la matriu A ha de satisfer: A*X(1)=X(2), A*X(2)=X(3), A*X(3)=X(4).

En aquest cas calulem la solució: A=[X(2),X(3),X(4)]*inv[X(1),X(2),X(3)]. Compararem la matriu A amb la que ha donat lloc a la generació d'individus per veure la diferència.

Per disposar de valors, generem les dades de 4 generacions a partir de la matriu original A.

x=[100;200;50]; %punt inicial
X=x;
N=3; %numero d'iteracions
for i=1:N
    xNext=A*x;
    x=xNext;
    X=[X,x]; %guardem tots els iterats
end
Ac=X(:,2:4)*inv(X(:,1:3)); %definició de la matriu dels sistema dinàmic
errorFloats = A-Ac %error respecte a la matriu original

errorFloats =

   1.0e-15 *

   -0.1464    0.0857    0.0555
   -0.0278    0.0034    0.0011
   -0.4119    0.3331    0.1110

Si fem que els valors siguin enters (no es compten els individus en nombres reals), la precissió no és la mateixa però s'ajusta més al que seria un cas real.

X=round(X); %fem les dades enteres (no comptem mai 1/2 individu o similar).
Ac=X(:,2:4)*inv(X(:,1:3)); %definició de la matriu del sistema dinàmic
errorEnters = A-Ac %error amb dades enteres respecte a la matriu original