Fourier Transform: Data approximation
From the work of Fourier(1768-1830) we know that every integrable function 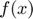 defined in
defined in ![$$[a,b]$](P4Fourier_eq11130704568637826070.png) can be approximate by a sum of trigonometric functions:
can be approximate by a sum of trigonometric functions:
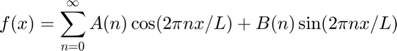 .
.
Here 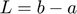 and because Fourier transform is specilly appropiate for periodic functions we can make a change of variables in the x variables a get the expressions for the Fourier coefficients as
and because Fourier transform is specilly appropiate for periodic functions we can make a change of variables in the x variables a get the expressions for the Fourier coefficients as
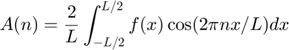
and analogously
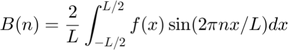
Compact representation:
If we define Phases as 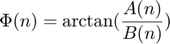 and amplitudes as
and amplitudes as 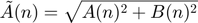 , Fourier transform can be also written as
, Fourier transform can be also written as
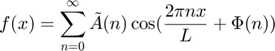 .
.
Contents
- A Simple Example:
- Compute Discrete Fourier Transform
- Compute Inverse Fourier Transform
- Frequencies and Magnitudes
- General Data Approach: Function through a data set.
- General Data Using Fast Fourier Transform from Matlab
- Fourier transform analysis
- Numerical trigonometric interpolation in a new point
- Discrete Fourier Transform Function
- Inverse Fourier Transform Function
- (c) Numerical Factory 2019
A Simple Example:
Consider one funcion 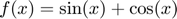 defined on
defined on ![$$[0,2\pi]$](P4Fourier_eq04024897143965832866.png) and we evaluate
and we evaluate 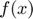 on
on 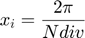 where
where 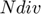 is the number of subdivisions.
is the number of subdivisions.
clear all; close all; Ndiv=8; h=2*pi/Ndiv; x=0:h:2*pi-h; %don't take last point (it is supposed to be the same as 0) f=sin(x)+cos(x); N=length(f);
Compute Discrete Fourier Transform
For N values we consider the points in the interval [-N/2, N/2] (this is more stable from a numerical point of view) and we approximate the integral by the sumatory (trapezoidal's rule).
By deffault we compute as many Fourier coefficients than number of points.
for k=0:N-1 sumA=0; sumB=0; for j=0:N-1 sumA=sumA+f(j+1)*cos(2*pi*j*(k-N/2)/N); sumB=sumB+f(j+1)*sin(2*pi*j*(k-N/2)/N); end A(k+1)=sumA/N; B(k+1)=sumB/N; end
Compute Inverse Fourier Transform
Once we have the Fourier coefficients we can use the Fourier series to approximate the true value f at each point.
We increase the order approximation to visualize convergence of the sumatory. Notice that only 3 coefficients are enought for this particular function
for order=1:N-1 plot(x,f,'o-'); %plot the original function hold on; for k=0:N-1 sum=0; for j=0:order sum=sum+A(j+1)*cos(2*pi*k*(j-N/2)/N)+B(j+1)*sin(2*pi*k*(j-N/2)/N); end faprox(k+1)=sum; end plot(x,faprox,'*-'); %plot the approximated points Error(order)=max(abs(f-faprox)); end hold off; disp('Error at each order approximation'); Error'
Error at each order approximation
ans =
1.4142
1.4142
0.7071
0.7071
0.0000
0.0000
0.0000

Frequencies and Magnitudes
We can represent the frequences space and the associated magnitudes from the previous formulas
for i=1:N Atilde(i)=sqrt(A(i)^2+B(i)^2); Phi(i)=atan(B(i)/A(i)); end figure() subplot(2,1,1) stem(-N/2:N/2-1,Atilde) xlabel('frequency');ylabel('amplitude') subplot(2,1,2) stem(-N/2:N/2-1,Phi) xlabel('frequency');ylabel('phase angle')

General Data Approach: Function through a data set.
Consider now that you have a set of measure data and you want to compute a function passing through these data. The Fourier approximation allow us to compute this function.
We will define (at the bottom of this document) the two functions:
- Discrete Fourier Transform: function fcoeff=DiscFourierTrans(f,N)
- Inverse Fourier Transform: function faprox=invFourierTrans(fcoeff,N,order)
%Consider a set of data values f=[10.7083 9.7003 8.9780 8.4531 8.1653 8.2633 8.8795 9.9850 11.3289 12.5172 13.2012 13.2720 12.9435 12.6647 12.8940 13.8516 15.3819 17.0033 18.1227 18.3039 17.4531 15.8322 13.9056 12.1154]; x=0:length(f)-1; % here x is just the enumeration of the data values. N=length(x); fcoeff=DiscFourierTrans(f,N); order=15; %try order = 13, 14 to see the different approximation faprox=invFourierTrans(fcoeff,N,order); figure() plot(x,f,'o-'); %plot the approximated points hold on; plot(x,faprox,'*-'); %plot the approximated points

General Data Using Fast Fourier Transform from Matlab
We solve the same previous example but using now Matlab function Fast Fourier Transform (fft)
Fourier transform analysis
P1 = fft(f)/N; %fast Fourier transform P2=fftshift(P1); % You can recover the real coefficients fcoeff=[real(P2),-imag(P2)]; order=15; faprox=invFourierTrans(fcoeff,N,order); %using our function % or you can use the compact Fourier formula amp=abs(P2); % amplitude for complex variables phi = angle(P2); % phase angle for complex variables for k=0:N-1 sum=0; for j=0:order sum=sum+amp(j+1)*cos(2*pi*k*(j-N/2)/N+phi(j+1)); end faproxCompact(k+1)=sum; end figure() title('Now using fft') plot(x,f,'s-'); %plot the approximated points hold on; plot(x,faprox,'d-'); %plot the approximated points plot(x,faproxCompact,'*-'); %plot the approximated points

Numerical trigonometric interpolation in a new point
Once we have the Fourier approximation of a set of data, we can use it to approximate the corresponding value for an unknown point not belonging to the data set.
We can use different order approximation and see how the new value behaves. Below we show for the point 10.5 (not in the original table) how the approximations of different Fourier order fits the original interpolated curve. For the maximum order (15) the interpolated value is on the curve.
point=10.5; order=[12,13,15]; for i=1:3 sum=0; for j=0:order(i) sum=sum+amp(j+1)*cos(2*pi*point*(j-N/2)/N+phi(j+1)); end fvalue(i)=sum; end xx=point*ones(3,1); % just to plot plot(xx,fvalue','sm'); %plot the approximated points

Discrete Fourier Transform Function
function fcoeff=DiscFourierTrans(f,N) for k=0:N-1 sumA=0; sumB=0; for j=0:N-1 sumA=sumA+f(j+1)*cos(2*pi*j*(k-N/2)/N); sumB=sumB+f(j+1)*sin(2*pi*j*(k-N/2)/N); end A(k+1)=sumA/N; B(k+1)=sumB/N; end fcoeff=[A;B]'; end
Inverse Fourier Transform Function
function faprox=invFourierTrans(fcoeff,N,order) if (order >=N), order=N-1; end; A=fcoeff(:,1); B=fcoeff(:,2); for k=0:N-1 sum=0; for j=0:order sum=sum+A(j+1)*cos(2*pi*k*(j-N/2)/N)+B(j+1)*sin(2*pi*k*(j-N/2)/N); end faprox(k+1)=sum; end end
(c) Numerical Factory 2019
(see this video for more intuition https://www.youtube.com/watch?reload=9&v=spUNpyF58BY )