1D-Interpolation of a set of measures

When we collect data from an experiment, we get a set of mesured values 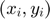. Interpolate these values means to compute a Polynomial (of degree one less than the number of measures) which goes through all the points.

Matlab uses the polyfit and polyval functions for doing that.

Contents

Example with 4 points

x=[0,1,2,3];
y=[1,3,5,2];

p=polyfit(x,y,3) % polynomial as a vector from max power to less one.
                 % p=p(1)x^3+p(2)x^2+p(3)x+p(4)

xx=0:0.1:3; %points to plot the polynomial
yy=polyval(p,xx);

plot(xx,yy)
hold on;
plot(x,y,'ro')
hold off;

p =

   -0.8333    2.5000    0.3333    1.0000

Approximation of a Function

We will use different strategies of approximating a function from only few points.

Let's consider the function:

in the domain [-1,1].

Take some points x=-1:0.2:1 used for approximating this function with a polynomial of different degree.

Compute points

close all
a=-1;
b=1;
% Define an Inline function
f=@(x) 1./(1+25*x.^2);
% Approximation points
x=a:0.2:b;
y=f(x);
% More points to represent the original function
xOrig=a:0.01:b;
yOrig=f(xOrig);
figure()
plot(xOrig,yOrig,'-.') %original function
hold on;
plot(x,y,'o','Marker','o','MarkerFaceColor','red'); %approximation points

Polyfit degree 3 function

We plot together the original function, approximation points and the approximation polynomial.

figure()
plot(xOrig,yOrig,'-.') %original function
hold on;
plot(x,y,'o','Marker','o','MarkerFaceColor','red'); %approximation points
p=polyfit(x,y,3);
yyy=polyval(p,xOrig); %values of the polynomial in all the original points
plot(xOrig,yyy,'-.b')
title('Degree 3 approximation');
hold off

Polyfit degree 7 function

same as before but using degree 7 polynomial.

figure()
plot(xOrig,yOrig,'-.')
hold on;
plot(x,y,'o','Marker','o','MarkerFaceColor','red');
p=polyfit(x,y,7);
yyy=polyval(p,xOrig); %values of the polynomial in all the original points
plot(xOrig,yyy,'-.b')
title('Degree 7 approximation');
hold off

Interpolation Polynomial: Polyfit degree 10 function

same as before but using degree 10 (= npoints -1) polynomial.

One can see the Runge Phenomenon at the beginning and final of the interval

figure()
plot(xOrig,yOrig,'-.')
hold on;
plot(x,y,'o','Marker','o','MarkerFaceColor','red');
p=polyfit(x,y,10);
yyy=polyval(p,xOrig); %values of the polynomial in all the original points
plot(xOrig,yyy,'-.b')
title('Degree 10 approximation');
hold off

1D Polygonal approximation

Use a polygonal approximation function when using more points.

figure()
xp=a:0.1:b;
yp=f(xp);
plot(xp,yp,'o','Marker','o','MarkerFaceColor','red');
hold on;
plot(xOrig,yOrig,'-.')
yyp=interp1(xp,yp,xOrig); %only substitution is possible
plot(xOrig,yyp,'b')
title('1D polygonal approximation');
hold off

Spline

Use a spline approximation function when using more points.

figure()
xs=a:0.1:b;
ys=f(xs);
plot(xs,ys,'o','Marker','o','MarkerFaceColor','red');
hold on;
plot(xOrig,yOrig,'-.')
yys=spline(xs,ys,xOrig); %only substitution is possible
plot(xOrig,yys,'b')
title('1D spline approximation');
hold off

Subplot images

This can help to present results together

figure()
degree=[3,5,7,10];
for i=1:size(degree,2)
    subplot(3,2,i)
    plot(x,y,'o','Marker','o','MarkerFaceColor','red');
    hold on;
    plot(xOrig,yOrig,'-.')
    p=polyfit(x,y,degree(i));
    yyy=polyval(p,xOrig);
    plot(xOrig,yyy,'-.b')
    if (degree(i) < 10)
        title(['Degree ', num2str(degree(i)),' approximation']);
    else
        title(['Degree ', num2str(degree(i)),' interpolation']);
    end
    axis([-1,1,-0.2,1])
    hold off
end
% Polygonal
subplot(3,2,5)
plot(xp,yp,'o','Marker','o','MarkerFaceColor','red');
hold on;
plot(xOrig,yOrig,'-.')
yyp=interp1(xp,yp,xOrig); %only substitution is possible
plot(xOrig,yyp,'b')
title('1D polygonal approximation');
hold off
%Spline
subplot(3,2,6)
plot(xs,ys,'o','Marker','o','MarkerFaceColor','red');
hold on;
plot(xOrig,yOrig,'-.')
yys=spline(xs,ys,xOrig); %only substitution is possible
plot(xOrig,yys,'b')
title('1D spline approximation');
hold off

Exercise:

Compute the mean and maximum error between the original curve and their approximation according to the polynomial degree for the measure points x=a:0.2:b and y=f(x). (Use all plotted points, xx=a:0.01:b to compute errors).

   Degree   meanError  maxError

   3.0000    0.1583    0.5159

   5.0000    0.1119    0.3448

   7.0000    0.0797    0.2154

   9.0000    0.0722    0.2392

Published with MATLAB® R2018a