EDPs: Solució de l'Equació de la Calor per Diferències Finites.
Veiem un exemple de solució numèrica d'una Equació en Derivades Parcials, en aquest cas de l'equació de la Calor.
Per aproximar numèricament les derivades d'una funció en un punt, utilitzen el que s'anomenen esquemes de diferències finites.
Contents
Diferencies Finites 1D
Es poden utilitzar diversos esquemes per calcular la derivada. Depenent de l'esquema escollit, la precissió serà millor.

- Diferències endavant: error

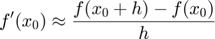
- Diferències centrades: error


- Segona Derivada. Diferències centrades: error

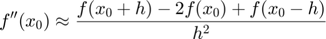
Derivades Parcials. Diferencies Finites 2D
Les derivades parcials de segon ordre (les de primer orde es farien de manera anàloga) s'aproximen per:
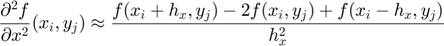
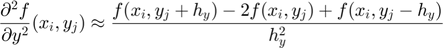

Dominis rectangulars 2D
Si tenim un domini rectangular per poder aplicar diferències finites hauríem de dividir-lo en punts equiespaiats. Un exemple amb el que estem acostumats a treballar és la descomposició en píxels d'una imatge. Carregar una imatge amb Matlab es fa així:
Aorig = imread('coins.png'); %llegim la imatge original imshow(Aorig); %mostrem la imatge original A = im2double(Aorig); %Per defecte el pixels son enters de 8 bits. %Per fer operacions els passem a doubles (no es %nota visualment)

Aplicació: difuminat d'una imatge a partir de l'eq. de la calor
L'equació que modela la distribució de temperatures al llarg del temps és
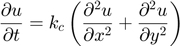
on la funció  depèn del temps i de les variables espaials.
depèn del temps i de les variables espaials.
Per simular l'evolució en el temps de la temperatura ens cal partir d'una distribució inicial de les temperatures. En aquest cas agafarem la imatge anterior (en tons de gris) i assimilem a temperatura el valor de intensitat de gris en cada píxel. Així, els píxels més blans seran els més calents.
El Matlab permet visualitzar aquestes temperatures creant una imatge 3D amb les instruccions d'aquí sota (gireu el gràfic 3D prement el botó circular de la finestra de Matlab i movent el ratolí)
figure(2) %imatge de distribució inicial de temperatures
x=1:size(A,2);
y=1:size(A,1);
[X,Y]=meshgrid(x,y);
mesh(X,Y,A)
colormap(jet);

Evolució Temporal de les Temperatures
A partir de la distribució inicial de temperatures. Apliquem l'eq. de la calor sobre la xarxa de píxels i veiem els efectes sobre la temperatura. Per això farem servir les diferències finites endavant de primer ordre pel terme de derivada temporal i les diferències centrades de segon ordre per les derivades espaials.
L'esquema quedaria (escribint només la dependència temporal i espaial respectivament)

En el nostre cas les valors  (la distància és un píxel) i prenem
(la distància és un píxel) i prenem 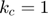 i
i 
Tenint en compte que el terme que volem calcular és 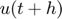 (la temperatura en el següent instant). Utilitzarem la notació
(la temperatura en el següent instant). Utilitzarem la notació  i podem aïllar aquest terme:
i podem aïllar aquest terme:

En el nostre cas la u són els valors de la imatge A i simulem l'evolució fins a temps=4
[m,n]=size(A); %mides d'A AA=A; %aquí fem servir A=u(t) i AA=u(t+h) (la inicialitzem igual a A) dt=0.1; tfin=4; for t=0:dt:tfin %recorrem fins el temps final for j=2:n-1 %recorrem tots els píxels, però evitem els de la vora for i=2:m-1 AA(i,j)=A(i,j)+dt*(A(i,j+1)+A(i+1,j)+A(i,j-1)+A(i-1,j)-4*A(i,j)); end end A=AA; %actualitzem el valor de les temperatures end
Resultats en passar el temps
figure(3) %imatge de distribució final de temperatures
imshow(A)
mesh(X,Y,A)
colormap(jet);

Reinterpretem com imatge i veiem que ha passat
figure(4) %imatge final, queda difuminada
imshow(A)
