Integració Numèrica d'EDOs

Mostrem un exemple de com s'han d'introduir les EDO's en el Matlab i com es crida el mètode d'integració numèrica (ode45 que és un RK45F) que segueix la trajectoria de la solució a partir d'un punt inicial. En tractar-se d'un mètode amb control automàtic de pas, no cal passar-li l'increment de temps per cada pas.

Sistema d'EDOs d'exemple: Moviment Harmònic Simple
Equacions Diferencials
Valors inicials
Crida a l'integrador numèric: ode45 (Runge-Kutta-Felberg 4-5)
Gràfiquem les solucions:
Multiples condicions incials
Exercici:

Sistema d'EDOs d'exemple: Moviment Harmònic Simple

Exemple d'integració d'un sistema d'EDOs amb t variable independent i 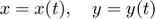$x=x(t), \quad y=y(t)$ .

L'equació diferencial és una EDO de segon ordre:

$$x'' = -x$ .

Escrita com a sistema d'equacions diferencials de primer ordre:

$$x'=y, \quad y'=-x$ .

Sempre caldrà donar una condició inicial:

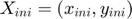
$X_{ini} =(x_{ini}, y_{ini})$

Equacions Diferencials

Hem de tenir en compte la notació X=[X(1), X(2)]=[x, y]

dx=@(x,y) y; %cada edo s'escriu com una funció inline
dy=@(x,y) -x;
% Ara ho escrivim com un sistema d'EDOs (seria una funció de funcions)
% Obs. Tot i que no sempre les edos depenen del temps, se sol incloure la t
deriv=@(t,X) [dx(X(1),X(2)); dy(X(1),X(2))]; %les eq. per files

Valors inicials

Xini=[1,0];
rangTemps=[0,20]; %[tini,tfin] és el temps de càlcul de la solució

Crida a l'integrador numèric: ode45 (Runge-Kutta-Felberg 4-5)

[t,X]=ode45(deriv,rangTemps,Xini);

% Podem utilitzar aquestes dues línies de sota per tenir
% més control sobre la precisió en la solució (farà molts més punts)
%
% opcions=odeset('AbsTol',1.e-8,'RelTol',1.e-10);
% [t,X]=ode45(deriv,rangTemps,Xini,opcions);

numPunts = length(t)

numPunts =

   121

Gràfiquem les solucions:

Hem de tenir en compte que X=[x(t), y(t)] és una taula de n files i 2 columnes

%------------------------------------
% Dibuixem les grafiques
%------------------------------------
% Característiques de la finestra de dibuix
    fig1=figure;
    set(fig1,'Name','INTEGRACIO EDOs',...
        'units', 'pixels','Position', [200, 50, 400, 600],...
        'NumberTitle','off','Resize','on');
%
%  Gràfiques de la solució
% --------------(t,x(t)) les x's en funció del temps
subplot(3,1,1);
    plot(t,X(:,1));
    xlabel('temps');
    ylabel('x');
% --------------(t,y(t)) les y's en funció del temps
subplot(3,1,2);
    plot(t,X(:,2));
    xlabel('temps');
    ylabel('y');
% --------------(x(t),y(t)) les x's i les y's (retrat de fases)
subplot(3,1,3);
    plot(X(:,1),X(:,2));
    xlabel('x');
    ylabel('y');
    axis equal;

Multiples condicions incials

Podem calcular de forma simultània moltes solucions amb condicions inicials diferents. En aquest exemple, cada solució serà una circumferència diferent.

Xini=[1,0; 0.5,0; 1.5,0];
numCI=size(Xini,1);
figure(); %obrim una nova finestra de dibuix
for i=1:numCI
    [t,X]=ode45(deriv,rangTemps,Xini(i,:));
    plot(X(:,1),X(:,2));
    hold on;
    xlabel('x');
    ylabel('y');
    axis equal;
end